題目

You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].

Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:

  • 0 <= j <= nums[i] and
  • i + j < n

Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].

Example 1

1
2
3
Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2

1
2
Input: nums = [2,3,0,1,4]
Output: 2

解釋題目

給你一個 array，叫做 nums，可以把 nums 想像成一個樓梯，每一層樓都是用 index 來表示，起始位置會是第 0 層，而樓梯上的數字代表可以前進的最大步數。跟 前一題 很像，但這題的前提是: 一定可以走到頂樓，只是要回傳最少步伐，最後要回傳步數。

思路 (1) 動態規劃

  1. 用動態規劃的方式解題，前一題 是如果能走到 i 樓層，我就去計算在第 i 樓能走到的最遠距離。所以把 dp [i] 設定為可以達到 i 樓層的的布林值。但是，此題的dp[i] 要設定成能跳到第 i 樓的最少步數。

  2. 一開始我只知道 dp[0] 是 0，因為不用走，其他層 dp[i] 不知道會要跳幾步，所以先給無限大 float('inf')

  3. dp 在這題的想法是，每當我跳到第 i 層時，我從第 i 層跳到第 j 層，只要 1 步。

  4. 以 [2, 3, 1, 1, 4] 為例。當我跳到第 0 層時，我可以從第 0 層可以跳到第 1 或第 2 層，而且只要 1 步，因此步數會是 dp[0] + 1。所以，我今天要比較的是:

    • 跳到 1 樓的最小步數比較少 ( 也就是 dp[1] 的設定) ，還是從我當前樓層 dp[i] 多跳 1 步 比較少 ( 也就是 dp[0] + 1 )
    • 跳到 2 樓的最小步數比較少 ( 也就是 dp[2] 的設定) ，還是從我當前樓層 dp[i] 多跳 1 步 比較少 ( 也就是 dp[0] + 1 )

    別忘記我們的定義 dp[i] 是能 跳到第 i 樓的最少步數

  5. 想通了這個概念，應該就大致理解 dp 在這題的應用。還沒想通可以繼續思考: 當我跳到第 1 層時，我可以從第 1 層可以跳到第 2、 3 、4 層，而且只要 1 步，因此步數會是 dp[1] + 1。所以，我今天要比較的是:

    • 跳到 2 樓的最小步數比較少 ( 也就是 dp[2] 的設定) ，還是從我當前樓層 dp[i] 多跳 1 步 比較少 ( 也就是 dp[1] + 1 )
    • 跳到 3 樓的最小步數比較少 ( 也就是 dp[3] 的設定) ，還是從我當前樓層 dp[i] 多跳 1 步 比較少 ( 也就是 dp[1] + 1 )
    • 跳到 4 樓的最小步數比較少 ( 也就是 dp[4] 的設定) ，還是從我當前樓層 dp[i] 多跳 1 步 比較少 ( 也就是 dp[1] + 1 )

  6. 表格化如下，一開始的 dp 值都是設定無限大。

    當前樓層 i 跳的範圍 比較跳到 j 樓最少步數 dp[j] &
    當前樓層多跳一步 dp[i] + 1    		 比較的結果
    0 1 dp[1] = min(dp[1], dp[0] + 1) min(inf, 0+1) = 1
    2 dp[2] = min(dp[2], dp[0] + 1) min(inf, 0+1) = 1
    1 2 dp[2] = min(dp[2], dp[1] + 1) min(1, 1+1) = 1
    3 dp[3] = min(dp[3], dp[1] + 1) min(inf, 1+1) = 2
    4 dp[4] = min(dp[4], dp[1] + 1) min(inf, 1+1) = 2
    2 3 dp[3] = min(dp[3], dp[2] + 1) min(2, 1+1) = 2
    3 4 dp[4] = min(dp[4], dp[3] + 1) min(2, 2+1) = 2

  7. 注意: 當樓層數 < 2 時，也就是只有 1 樓時，就不需要跳躍了。

  8. 此解法的時間複雜度 O(n^2)，空間複雜度 O(n)。

程式碼 (1) 動態規劃

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return 0  # 不需要跳躍

        # 初始化 DP 陣列
        dp = [float("inf")] * n # 無限大
        dp[0] = 0  # 起點不需要跳躍

        # 填充 DP 陣列
        for i in range(n):
            for j in range(i + 1, min(i + 1 + nums[i], n)):  # i 能跳到的範圍
                dp[j] = min(dp[j], dp[i] + 1)

        return dp[-1]

思路 (2) Greedy

  1. 用貪婪法解題，我感覺比較抽象。貪婪法主要的想法是

    • 紀錄每走一層樓時，能到達到的最遠距離，此步驟可以確認每一步都有計算到
    • 甚麼時候要跳，當我達到前一次跳躍的位置時，我就必須要跳，跳的距離是，我經過的樓層中所記綠到的最遠距離

  2. 以 [2, 3, 1, 1, 4] 為例，我從第一樓開始跳，一開始都還沒跳，所以前一次跳躍的位置 ( last_jump_index ) 是 0。

  3. 一開始就要跳了，但此時只記錄到第 0 層樓可以跳的最遠距離，也就是 i + nums[i]，所以 i = 0 時，最遠距離 ( farest ) 是 2。

    • 此時，我要跳到最遠距離 2，所以 last_jump_index 是 2。

  4. 接著，記錄到第 1 樓時，可跳躍的最遠距離是 1 + 3 = 4，比 2 還大，所以最遠距離 ( farest ) 變成 4。

  5. 接著，記錄到第 2 樓時，可跳躍最遠距離是 2 + 1 = 3，比 4 還小，所以最遠距離 ( farest ) 還是 4。

    • 此時，我不得不跳了，因為已經達到前一跳的位置 2 ，所以我要從 index 2 跳到最遠距離 4 ，所以 last_jump_index 是 4。

  6. 之後以此類推即可，我們還可以在迴圈加個條件，就是當 last_jump_index >= n 時，就終止迴圈，因為已經抵達了。

雖然這樣想比較抽象，因為我的跳躍是抵達前一次跳躍的 last_jump_index 時，記錄到的最遠距離， 0 -> 2 -> 4，但其實我們真正跳躍的樓層是 0 -> 1 -> 4，因為我只要記錄我會跳幾次，從哪層樓跳並不重要。

程式碼 (2) Greedy

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        farest = last_jump_index = jump = 0
        for i in range(n - 1):
            if i == last_jump_index:
                farest = max(farest, i + nums[i])
                jump += 1
                last_jump_index = farest
            
            if last_jump_index >= n - 1:
                break
        return jump

思路 (3) BFS

  1. 用 BFS 解題，BFS 是 Breadth First Search 廣度優先的縮寫，主要是一層一層去搜尋，再慢慢往下一層搜尋。這題可用 BFS，主要是因為我們要去計算每一層可以到達的所有節點。

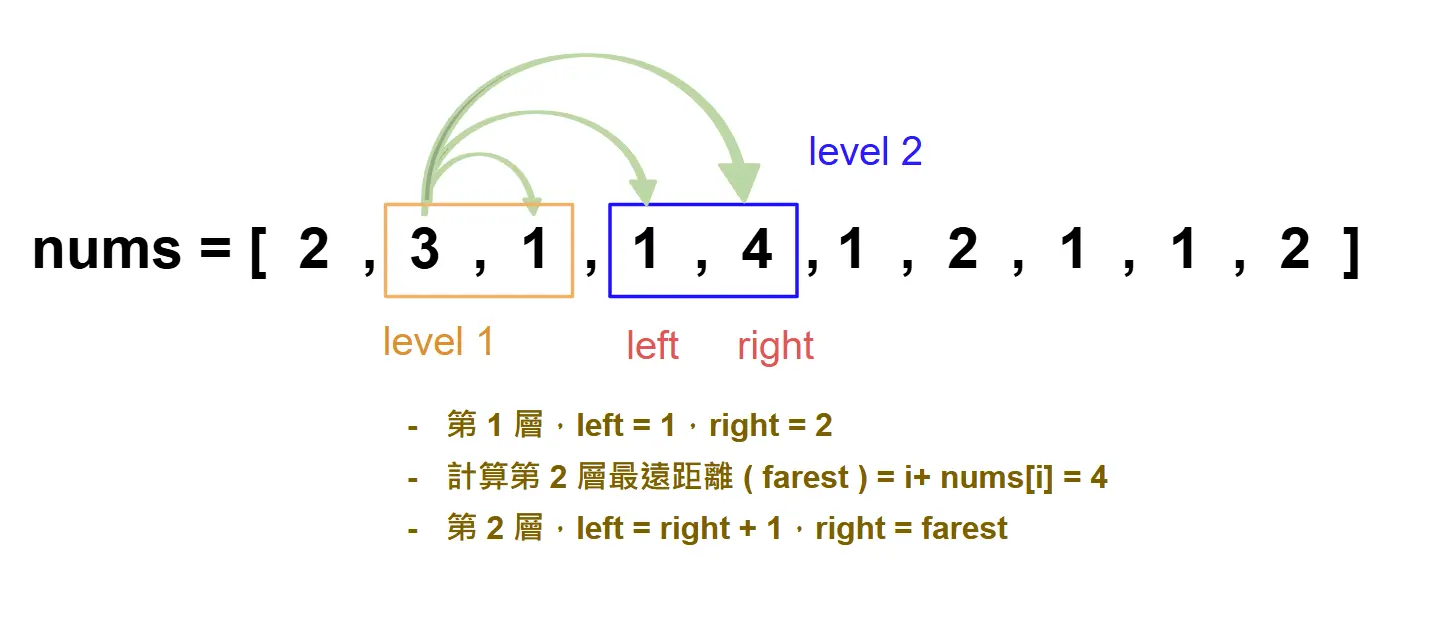
  2. 以 [2, 3, 1, 1, 4, 1, 2, 1, 1, 2] 為例，從第「零」階 2 出發，要嘛走到第「一」階、要嘛走到第「二」階，所以 第一階 ~ 第二階 是 第一層 的範圍。也就是說:

    從起始點走到第一層，只需要 1 步。而第一、二階是起始點可以抵達的所有節點。

  3. 此時，我們要遍歷第一層的所有數字，找出第二層的範圍。第「一」階 3 最遠可以走到第「四」階；第「二」階 1 最遠可以走到第「三」階。因為第二階已經在第一層的範圍內了，所以 第二層 的範圍是 第三階 ~ 第四階。也就是說:

    從第一層走到第二層，也只需要一步。而第三、四階是從第一層可以抵達的所有節點。

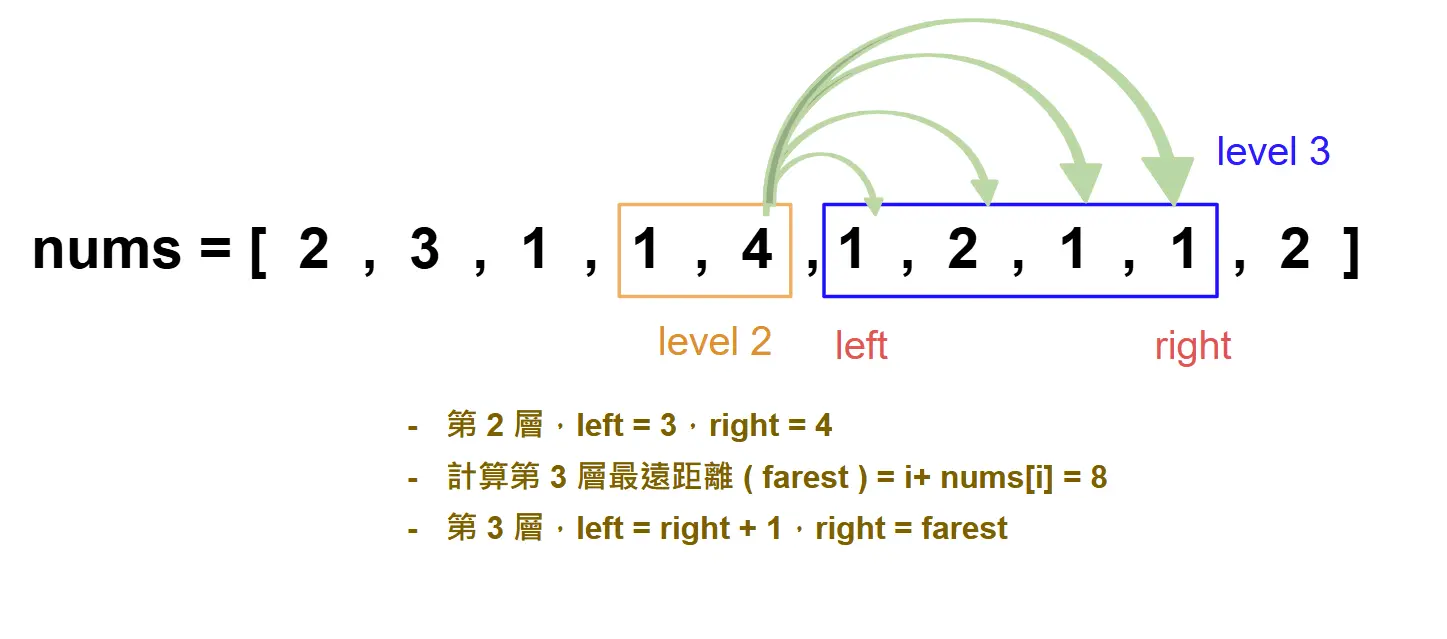
  4. 此時，似乎有一些端倪。我們就是要 尋找每一層的起始點跟終點。而每一層的範圍可以想像是一個 window 的概念，每一層就是走一步。而 終止的條件就是: 在某一層的終點碰到最後一階。

  5. 所以每一層的起始點 ( left ) 是左指針，終點 ( right ) 是右指針。終止條件是當 right < len(nums) - 1 時，因為當 right 碰到頂樓，就代表不用再走了。

  6. 一開始，左右指針都在第「零」階的位置。所以第 0 層的範圍會是 range( left, right + 1 ) ，要包含右指針 ( right )，所以 right 要 + 1，因為要去計算第 0 階可以走到的所有節點範圍。

  7. 在每一層的範圍裡，要去計算最遠距離 ( farest )，會是每個 range 裡的 i + nums[i]，而下一層起始範圍就會是上一層終點的下一個位置，也就是 left = right + 1，而下一層起始範圍就會是最遠距離 ( farest )。

  8. 每經過一層，跳躍次數 ( jump ) 就要 + 1 次。

圖像拆解

步驟拆解 1

步驟拆解 2

步驟拆解 3

步驟拆解 4

程式碼 (3) BFS

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        left = right = farest = 0
        while right < n - 1:
            for i in range(left, right + 1):
                farest = max(farest, i + nums[i])
            left = right + 1
            right = farest
            jump + = 1
        return jump